UA Part 6: Mappings - 6.8.1 Secure Channel Handshake

6.8.1 Secure Channel Handshake

The OPC UA Secure Conversation (UASC) mechanism described 6.7 is designed for use with asymmetric cryptography algorithms, such as RSA, that allow Public Keys to be used for encryption and for digital signatures. ECC is an asymmetric cryptography algorithm that only supports digital signatures. To accommodate algorithms like ECC, the UASC handshake needs to be modified to allow negotiation of inputs used for key derivation in 6.7.5 without making the keys available to eavesdroppers. This negotiation uses a Diffie Hellman algorithm defined in RFC 8422 and is shown in Figure 13.

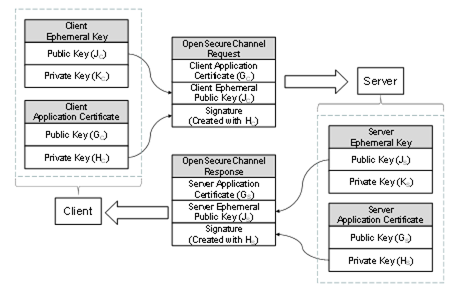
Figure 13 – ECC Key Negotiation

ApplicationInstance Certificates for ECC have a public-private key pair that are used to create and verify a digital signature. To negotiate the keys needed for the SecureChannel the Client generates a new key pair (JC, KC) and passes the Public Key (JC) in the request. After verifying the signature on the request, the Server generates a new key pair (JS, KS) and returns the Public Key (JS) in the response. The new key pairs are used each time a SecureChannel is negotiated and they are called EphemeralKeys.

ECC public-private key pairs are always based on a specific elliptic curve function which is used for the ECC calculations. Many curves exist, however, ECC cryptography libraries support a finite set of “named curves” to allow for better interoperability. Each OPC UA SecurityPolicy defined in OPC 10000-7 specifies exactly one named curve which is used for the EphemeralKeys.

Each ECC ApplicationInstance Certificate is also based on a named curve. Each SecurityPolicy specifies a list of named curves which are permitted for use in the ApplicationInstance Certificate. This list always includes the named curved used for the EphemeralKey, however, it may allow other named curves. OPC UA applications that support ECC SecurityPolicies will need to support multiple ApplicationInstance Certificates.

ECC Public Keys and digital signatures are the output of an ECC operation. The encoding of these outputs depends on the ECC curve and are described by the SecurityPolicy in OPC 10000-7.

Clause 6.7.4 specifies the contents of the OpenSecureChannel request and response messages. When using an ECC SecurityPolicy the ClientNonce is the Public Key for the Client’s EphemeralKey encoded using the Public Key encoding for the curve. Similarly, the ServerNonce is the Public Key for the Server’s EphemeralKey.

The encoding of the EphemeralKeys depends on the ECC curve used. For NIST and Brainpool curves the EphemeralKey is the x and y coordinate encoded as zero padded big-endian OctetString. For Edwards curves the EphemeralKey format is defined by RFC 7748.

The EphemeralKeys are used to calculate a shared secret by using the Private Key of an EphemeralKey and the Public Key of the peer’s EphemeralKey. The exact algorithm to calculate the shared secret depends on the ECC curve and is defined by the SecurityPolicy. This shared secret is then used to derive key data using the following algorithm from RFC 5869. Note that the algorithm is repeated here for clarity, however, the RFC is the normative source.

Step 1: Calculate Salts

ServerSalt = L | UTF8(opcua-server) | ServerNonce | ClientNonce

ClientSalt = L | UTF8(opcua-client) | ClientNonce | ServerNonce

Where

L is the length of derived key material needed encoded as a 16-bit little endian integer;
UTF8(label) is the UTF8 encoding of the string literal ‘label’;
ServerNonce is the Server EphemeralKey from the OpenSecureChannel response;
ClientNonce is the Client EphemeralKey from the OpenSecureChannel request;
| concatenates sequences of bytes;
Salt is a sequence of bytes.

Step 2: Extract

PRK = HMAC-Hash(Salt, IKM)

Where

HMAC uses a Hash function specified by the KeyDerivationAlgorithm;
IKM is the x-coordinate of the shared secret;
Salt is calculated in Step 1;
PRK is a pseudorandom output with length equal to the Hash size.

The encoding of the x-coordinate depends on the ECC curve used. For NIST and Brainpool curves the x-coordinate is encoded as a zero padded big-endian OctetString. For Edwards curves the coordinate format is defined by RFC 7748.

Step 3: Expand

N = ceil(L/HashLen)

T = T(1) | T(2) | T(3) | ... | T(N)

OKM = first L octets of T

where:

T(0) = empty string (zero length)

T(1) = HMAC-Hash(PRK, T(0) | Info | 0x01)

T(2) = HMAC-Hash(PRK, T(1) | Info | 0x02)

T(3) = HMAC-Hash(PRK, T(2) | Info | 0x03)

...

Where

HMAC uses a Hash function specified by the KeyDerivationAlgorithm;
PRK is the output from Step 1;
Info is a sequence of bytes;
L is the length of keying material needed;
0x01 is the number 1 encoded as a byte.
OKM is the output with length equal to L bytes.

The client keys are extracted from the keying material created with IKM=shared secret, Salt=ClientSalt and Info=ClientSalt as shown in Table 66.

Table 66 – Deriving Client Keys from Keying Material

Name	Offset	Length
ClientSigningKey	0	DerivedSignatureKeyLength
ClientEncryptingKey	DerivedSignatureKeyLength	EncryptionKeyLength
ClientInitializationVector	DerivedSignatureKeyLength + EncryptionKeyLength	InitializationVectorLength

The server keys are extracted from the keying material created with IKM=shared secret, Salt= ServerSalt and Info=ServerSalt as shown in Table 67.

Table 67 – Deriving Server Keys from Keying Material

Name	Offset	Length
ServerSigningKey	0	DerivedSignatureKeyLength
ServerEncryptingKey	DerivedSignatureKeyLength	EncryptionKeyLength
ServerInitializationVector	DerivedSignatureKeyLength + EncryptionKeyLength	InitializationVectorLength

The SymmetricEncryptionAlgorithm for the SecurityPolicy sets the EncryptionKeyLength and EncryptionBlockSize.

When using AuthenticatedEncryption, the SigningKey, EncryptingKey and InitializationVector are always calculated, however, only the EncryptingKey and InitializationVector are used. The only difference between Sign and SignAndEncrypt is the length of encrypted data which is zero when Sign is used. The process of signing and encrypting data with AuthenticatedEncryption is illustrated in Figure 14.

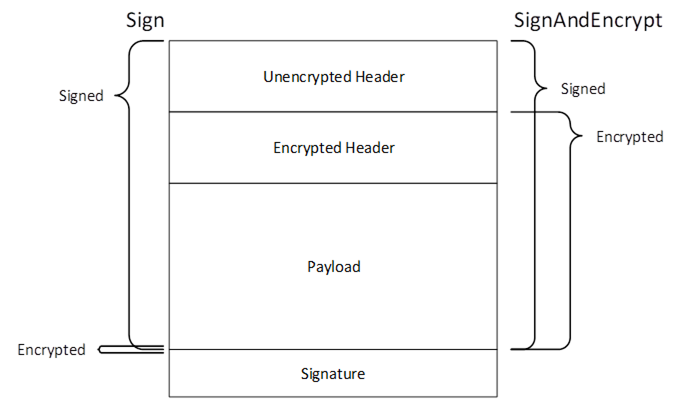
Figure 14 – Signing and Encryption with Authenticated Encryption

When using UnauthenticatedEncryption with Sign only the SigningKey needs to be computed, however, the length of the derived key material used to calculate the Salt shall be the same as the length of the derived key material used with SignAndEncrypt. The encryption algorithm is not used and the padding is zero length when using Sign mode. The process of signing and encrypting data with UnauthenticatedEncryption is illustrated in Figure 15.

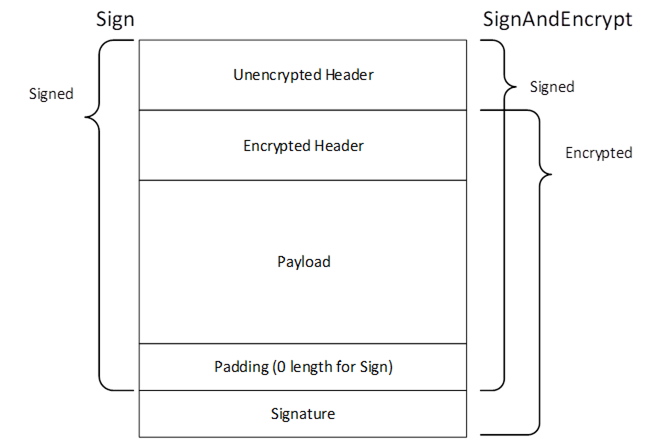
Figure 15 – Signing and Encryption with Unauthenticated Encryption

In addition, a unique InitializationVector is needed for each Message. This value constructed from the ClientInitializationVector or ServerInitializationVector where the first 8 bytes are XORed with the values in Table 68 encoded as described in 5.2.2.2.

Table 68 – Creating a Mask for the Initialization Vector

Name	Bytes	Length
TokenId	4	The TokenId specified in the SecurityHeader of MessageChunk being processed. It is encoded as a UInt32 as described in 5.2.2.2.
LastSequenceNumber	4	The SequenceNumber specified in the SequenceHeader of last MessageChunk sent in the same direction on the SecureChannel. The value is 0 to indicate there is no LastSequenceNumber for the first MessageChunk which is always the OpenSecureChannel Message. It is encoded as a UInt32 as described in 5.2.2.2.

The ClientInitializationVector is used when the Client encrypts the MessageChunk and the ServerInitializationVector is used when the Server encrypts the MessageChunk.

The LastSequenceNumber is the SequenceNumber from the previously sent Message which normally requires the previous Message to be decrypted. If the receiver processes incoming Messages in parallel it can calculate the expected SequenceNumber based on the order in which the encrypted Messages are received.

Once the keys are derived ECC SecureChannels behave the same as RSA SecureChannels.