The StandardDeviationPopulation Aggregate defined in Table 50 uses the formula:
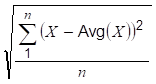
where X is each Good raw value in the interval, Avg(X) is the average of the Good raw values, and n is the number of Good raw values in the interval.
For every interval where n = 1, a value of 0 is returned.
If any non-Good values were ignored, the Aggregate quality is uncertain/subnormal.
All interval Aggregates return timestamp of the start of the interval. Unless otherwise indicated, qualities are Good, Calculated.
This calculation is for a full population where the calculation is done on the full set of data. Use StandardDeviationSample to calculate the standard deviation of a subset of the full population (5.4.3.37). An example would be when the underlying data is collected on an exception basis versus sampled from the data source.
Table 50 – StandardDeviationPopulation Aggregate summary
|
StandardDeviationPopulation Aggregate Characteristics |
||
|
Type |
Calculated |
|
|
Data Type |
Double |
|
|
Use Bounds |
None |
|
|
Timestamp |
StartTime |
|
|
|
||
|
StatusCode Calculations |
||
|
Calculation Method |
Custom Always Good |
|
|
Partial |
Set Sometimes If an interval is not a complete interval |
|
|
Calculated |
Set Always |
|
|
Interpolated |
Not Set |
|
|
Raw |
Not Set |
|
|
Multi Value |
Not Set |
|
|
|
||
|
StatusCode Common Special Cases |
||
|
Before Start of Data |
Bad_NoData |
|
|
After End of Data |
Bad_NoData |
|
|
No Start Bound |
No special handing required |
|
|
No End Bound |
No special handing required |
|
|
Bound Bad |
No special handing required |
|
|
Bound Uncertain |
No special handing required |
|