The position and orientation of objects in space is a general requirement that will be needed also by other companion specifications. Thus, we try to establish a general description.
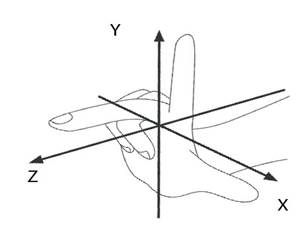
Figure 8 – Right handed cartesian coordinate system
Source: https://documentation.viewar.com/docs/additional_information/right-handed-coordinate-system
A frame describes the translation and rotation of an object relative to another frame (the base frame). Figure 9 shows a simple frame chain to clarify the notation. The frame A is the base of frames B and C. The frames B and C are based on frame A. Frame C is the base of frames D and E. The frames D and E are based on frame C.
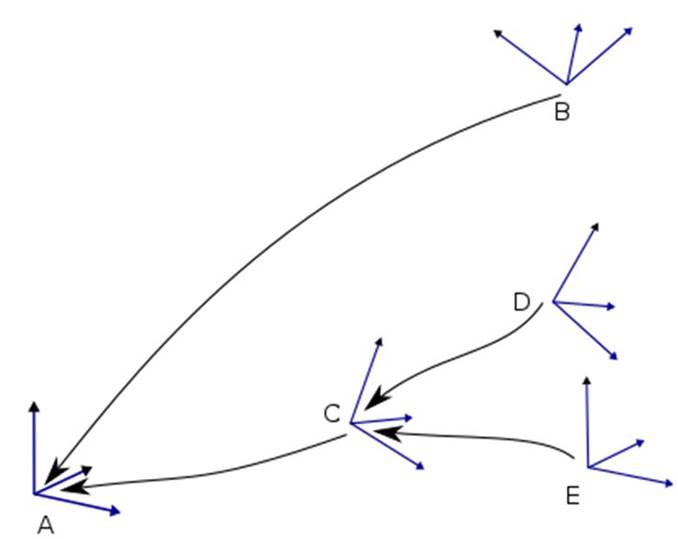
As shown in Figure 9 an arrow points from a frame to its base frame to visualize the frame chains. This arrow can be read as “The coordinates of frame B are specified in (or relative to) Frame A”. In addition to the coordinates of frame B you also need to know its base frame A.
The coordinates of a frame are represented by the three values P = (X, Y, Z) for the position and the three values O = (A, B, C) for the orientation.
P is the translation relative to the base frame. When the translation of a frame is 0 then the origins of the frame and its base frame coincide.
O is the orientation of the frame in yaw, pitch and roll notation (see also ISO 9787:2013 “Robots and robotic devices — Coordinate systems and motion nomenclatures” or Wikipedia article about Euler angles)
We use the notation of pre-multiplying rotation-matrices and column vectors.
Figure 10 shows the three elementary rotations A, B and C as specified in ISO 9787:2013.
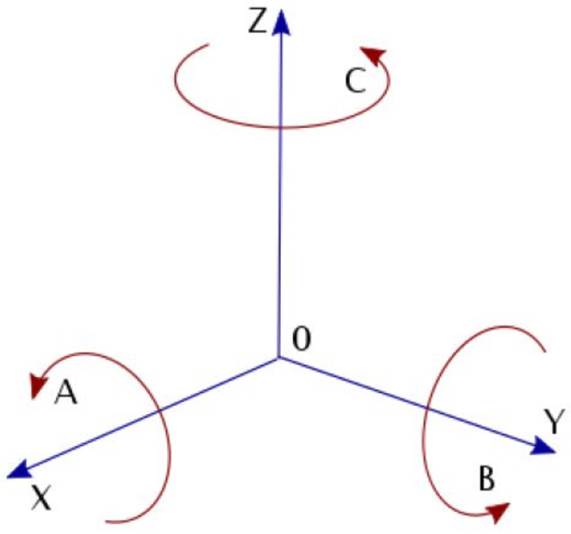
The elementary rotations correspond to the following rotation matrices:
A = roll = rotation about X axis
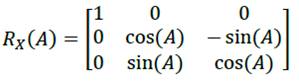
B = pitch = rotation about Y axis
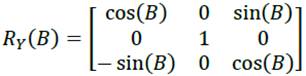
C = yaw = rotation about Z axis
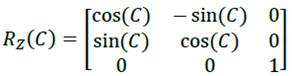
ISO 9787:2013 does not define the order of the rotations or the whether to use intrinsic or extrinsic rotations. Thus, we refer to the Wikipedia article here. It says that the intrinsic rotations z-y’-x″ are known as yaw, pitch and roll, giving the transformation matrix
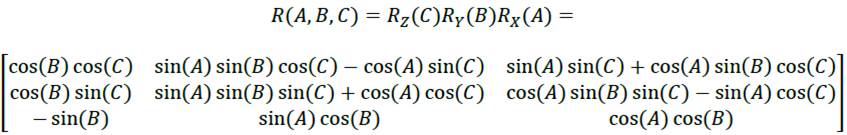
Figure 11 shows the three consecutive rotations:
1. Rotation about the Z axis (blue rotation; blue frame à green frame)
2. Rotation about the new Y axis (green rotation; green frame à red frame)
3. Rotation about the new X axis (red rotation; red frame à black frame)
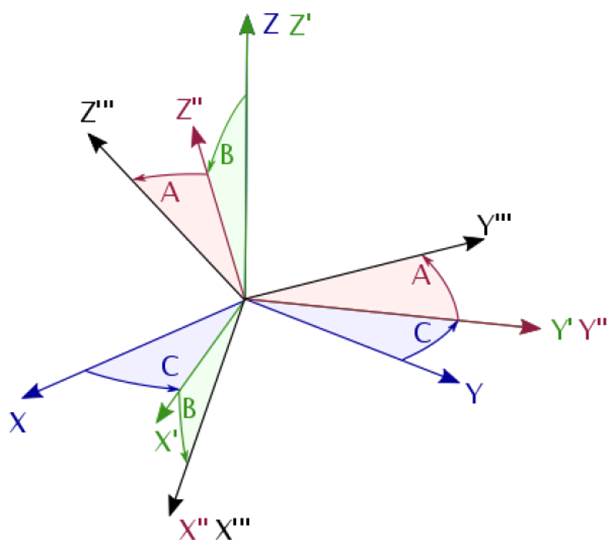
Figure 11 – Rotations of a frame
The extrinsic rotations x-y-z about the axis of the original fixed coordinate system result in the same transformation matrix. This is
1. Rotation about the X axis
2. Rotation about the original Y axis
3. Rotation about the original Z axis