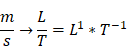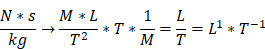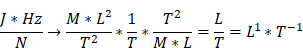The QuantityDimension Structure DataType describes the dimensionality of a kind of quantity in the context of a system of units. In the SI system of units, the dimensions of a kind of quantity are expressed as a product of the basic physical dimensions length (L), mass (M), time (T), current (I), absolute temperature (θ), amount of substance (N) and luminous intensity (J) as
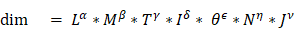 .
.
The rational powers of the dimensional exponents (α, β, γ, δ, ε, η, v), are positive, negative, or zero.
An additional dimensionless exponent is used for countable things that have no physical quantity assigned.
The QuantityDimension elements are defined in Table 53.
Table 53 – QuantityDimension DataType structure
|
Name |
Type |
Description |
|
QuantityDimension |
Structure |
|
|
MassExponent |
SByte |
Exponent of the dimension mass for the physical quantity. |
|
LengthExponent |
SByte |
Exponent of the dimension length for the physical quantity. |
|
TimeExponent |
SByte |
Exponent of the dimension time for the physical quantity. |
|
ElectricCurrentExponent |
SByte |
Exponent of the dimension electric current for the physical quantity. |
|
AmountOfSubstanceExponent |
SByte |
Exponent of the dimension amount of substance for the physical quantity. |
|
LuminousIntensityExponent |
SByte |
Exponent of the dimension luminous intensity for the physical quantity. |
|
AbsoluteTemperatureExponent |
SByte |
Exponent of the dimension absolute temperature for the physical quantity. |
|
DimensionlessExponent |
SByte |
Exponent for dimensionless quantities. |
Its representation in the AddressSpace is defined in Table 54.
Table 54 – QuantityDimension definition
|
Attribute |
Value |
|||||
|
BrowseName |
QuantityDimension |
|||||
|
IsAbstract |
False |
|||||
|
References |
NodeClass |
BrowseName |
DataType |
TypeDefinition |
Other |
|
|
Subtype of Structure defined in OPC 10000-5. |
||||||
|
Conformance Units |
||||||
|
Data Access Quantities Base |
||||||
For example, the dimension of the physical quantity kind
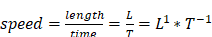 ,
,
the dimension of the physical quantity kind force is
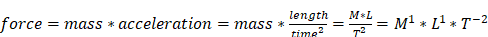 ,
,
and the dimension of the physical quantity kind “things (e.g., screws) per time” is
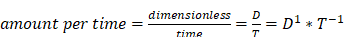 .
.
Table 55 – QuantityDimension examples
|
Name |
Values for speed |
Values for force |
Values for “things per time” |
|
QuantityDimension |
|
|
|
|
MassExponent |
0 |
1 |
0 |
|
LengthExponent |
1 |
1 |
0 |
|
TimeExponent |
-1 |
-2 |
-1 |
|
ElectricCurrentExponent |
0 |
0 |
0 |
|
AmoutOfSubstanceExponent |
0 |
0 |
0 |
|
LuminousIntensityExponent |
0 |
0 |
0 |
|
AbsoluteTemperatureExponent |
0 |
0 |
0 |
|
DimensionlessExponent |
0 |
0 |
1 |
The extended SI System of units includes derived units that are built as a product of base units. That makes it difficult to compare units as SI allows an unlimited number of “SI unit strings” to describe the same quantity.
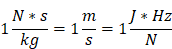
All 3 are valid SI representations of the quantity “speed” and therefore share the same quantity dimensions. A specific representation of a unit is often used to express details how the unit was measured. The dimension structure makes it much easier to identify and compare the kind of quantity of EU values.